Types of Angles: Vertical, Corresponding,

Video Lesson on Types of Angles: Vertical, Corresponding,

Types of Angles: Vertical, Corresponding, Alternate Interior & Others

In addition to basic right, acute, or obtuse angles, there are many other types of angles or angle relationships. In this lesson, we will learn to identify these angle relationships and discuss their measurements.

Angles are Everywhere

Have you ever looked at a sliced pizza and noticed that the beginning of each pizza slice was the same size? Did you ever take the time to wonder why that was? Or, have you ever examined the lines in a parking lot? While you may have noticed all the lines that form the parking spaces, did you ever think about the angles that were formed?

Well, if you haven't before, I'm sure you're thinking of them now. In every pizza and in every parking lot, there are many different angles and angle relationships. In this lesson, we are going to learn about these relationships, ways to identify the relationships and examine the measures of these angles.

Types of Angles

The first angle relationship that we will discuss is vertical angles. They are defined as a pair of nonadjacent angles formed by only two intersecting lines. They are known as 'Kissing Vs' and always have congruent measures. In the figure below, angles 1 and 3 are vertical, as well as angles 2 and 4.

Vertical angles are known as kissing Vs.

The second relationship is corresponding angles. They are considered to be in the same location at each point of intersection. For example, take a look at angles 1 and 3 below. They are both in the upper left corner. Another pair of corresponding angles is angles 6 and 8, which are both in the lower right corner.

Corresponding angles are at the same location on points of intersection.

Next we have alternate interior angles. Located between the two intersected lines, these angles are on opposite sides of the transversal. Angles 2 and 7 above, as well as angles 3 and 6 are examples of alternate interior angles.

Similarly, we also have alternate exterior anglesthat are located outside of the two intersected lines and on opposite sides of the transversal. An example of this relationship would be angles 1 and 8, as well as angles 4 and 5.

The last angle relationship is consecutive interior angles. These angles are located on the same side of the transversal and inside of the two lines. In the diagram above, angles 2 and 3 are consecutive interior angles, and so are angles 6 and 7.

With the exception of vertical angles, all of these relationships can only be formed when two lines are intersected by a transversal.

Determining Angle Relationships

With so many similarities, you may be wondering how to determine the relationship between angles formed by transversals and intersecting lines. All you have to do is ask yourself these three basic questions:

Are the angles in the same location at both points of intersection? This means that we want to know if they are both in the upper left, upper right, lower left, or lower right corners of the intersections. If you determine that they are in the same location, then these angles must be corresponding angles, and you are finished. If they are not corresponding angles, move on to questions 2 and 3.
Are the angles on the same side or opposite sides of the transversal? If they are on the same side, then the angles are considered consecutive. If they are on opposite sides, then the angles are considered alternate.
Are the angles inside or outside of the two intersected lines? If they are inside the two lines, then they will be classified as interior. If located outside the two lines, then the angles are considered to be exterior.

From here, we will combine our answers for questions 2 and 3 to determine the relationship between the angles.

Before we get into our examples, let's go ahead and discuss the relationship between the measures of these angles.

Angle Measures

As mentioned earlier, a pair of vertical angles will always be congruent. No matter what the diagram looks like, each pair of vertical angles will always have the same measurement. But, the story is a little different when observing corresponding, alternate interior, alternate exterior or consecutive interior angles. We cannot make any assumptions about their values unless we have one specific condition: parallel lines.

When the two lines intersected by the transversal are parallel, corresponding angles are congruent, alternate interior angles are congruent, alternate exterior angles are congruent, and consecutive interior angles become supplementary, which means they have a sum of 180 degrees.

Putting It All Together

Now that we are aware of these relationships and their measures, let's tie all of this information together by examining a couple of basic problems.

In the diagram below, please notice that line a is parallel to line b. Line c is the transversal. For our first example, the measure of angle 1 = 6x - 3 and the measure of angle 8 = 4x + 33. What is the value of x?

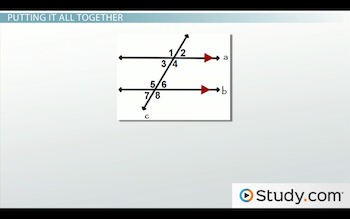
Diagram for example problems

Before we can solve this problem, we must determine the relationship between these two angles. Let's answer those three questions from earlier. For question 1, we notice that these angles are not in the same location. Angle 1 is in the upper left corner of the top intersection, and angle 8 is in the lower right corner of the bottom intersection, so they cannot be corresponding angles. Let's move to question 2. We see that these two angles are on opposite sides of the transversal, so we can classify them as alternate angles. In response to question 3, both angles are outside of the two lines and must be exterior angles. When we combine our answers to these questions, we can conclude that they are alternate exterior angles.

Since the two lines are parallel, we know that their measures must be equal. So, to solve for x, we will set 6x - 3 = 4x + 33. From here, we will subtract 4x from both sides and then add 3 to both sides to get 2x = 36. Once we divide both sides by 2, we will find that the value of x = 18.

For our next example, let angle 6 = 15y - 11 and angle 4 = 20y + 16. What is the measure of angle 7?

Before we can find the measure of the angle, we must first solve for y. To do this, let's begin by determining the relationship between the two angles. We will revisit the three questions from earlier. In response to question 1, we see that angle 4 and angle 6 are not in the same location at each intersection, so they are not corresponding angles. To answer question 2, they are on the same side of the transversal, which makes them consecutive angles. And, to address question 3, they are both within the two lines, which makes them interior. Therefore, we see that angles 4 and 6 are consecutive interior angles.

Since the two lines are parallel, we know that we should add these angles together and set them equal to 180. When we do, we get 15y - 11 + 20y + 16 = 180. Once we combine our like terms, we have 35y + 5 = 180. From here, we will subtract 5 from both sides to get 35y = 175, and then we will divide both sides by 35 to get y = 5.

Though this is a great start to our problem, we are not yet finished. We were asked to determine the measure of angle 7, even though we were only given information about angles 6 and 4. Let's find the connection between the angles.

In examining the picture, we notice that the vertex of angle 7 meets the vertex of angle 6. These two angles are nonadjacent and are formed by only two intersecting lines. By definition, these are vertical angles, and their measures must be congruent. Therefore, if we find the measure of angle 6, we will also know the measure of angle 7.

Since we know that y has a value of 5, we will substitute this into the equation for angle 6. We will see that angle 6 = 15(5) - 11. After we simplify, we see that angle 6 measures 64 degrees. As we stated before, angle 6 and angle 7 are congruent because they are vertical angles. Therefore, we can conclude that angle 7 is also 64 degrees.

Lesson Summary

In review, vertical angles are angles formed by the intersection of two lines while alternate interior angles, alternate exterior angles, corresponding angles and consecutive interior angles are formed by the intersection of two lines and a transversal.

Determining if angles are vertical requires simple observation, while determining other angle relationships can be done by asking yourself three questions: