Lesson: Chapter - 4

Exponents

An exponent defines the number of times a number is to be multiplied by itself. For example, in a^b, where a is the base, and b the exponent, a is multiplied by itself b times. In a numerical example, 2⁵ = 2 × 2 × 2 × 2 × 2. An exponent can also be referred to as a power: a number with an exponent of 2 is raised to the second power. There are some other terms that you should be familiar with:

• Base. The base refers to the 3 in 3⁵. It is the number that is being multiplied by itself however many times specified by the exponent.
• Exponent. The exponent (or power) is the 5 in 3⁵. The exponent tells how many times the base is to be multiplied by itself.
• Square. Saying that a number is “squared” means that it has been raised to the second power, i.e., that it has an exponent of 2. In the expression 6², 6 has been squared.
• Cube. Saying that a number is “cubed” means that it has been raised to the third power, i.e., that it has an exponent of 3. In the expression 4³, 4 has been cubed.

Common Exponents

It may be worth your while to memorize a few common exponents before the test. Knowing these regularly used exponents can save you the time it would take to calculate them during the test. Here is a list of squares from 1 through 10:

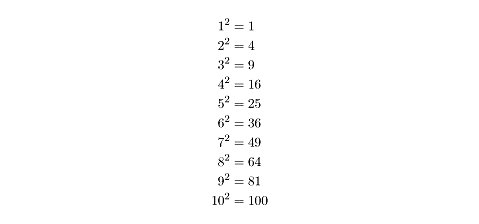
emorizing the first few cubes can be helpful as well:

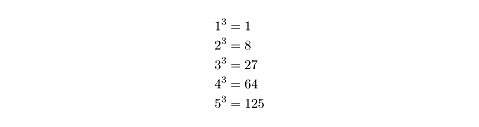
Finally, the first few powers of two are useful for many applications:

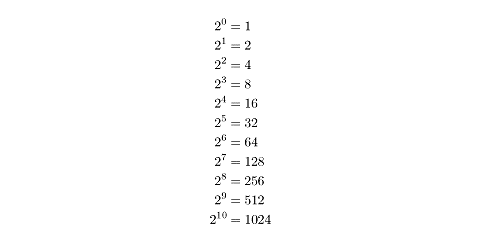
Adding and Subtracting Numbers with Exponents

In order to add or subtract numbers with exponents, you have to first find the value of each power, and then add the two numbers. For example, to add 3³ + 4², you must expand the exponents to get (3× 3 × 3) + (4 × 4), and then, finally, 27 + 16 = 43.

If you’re dealing with algebraic expressions that have the same bases and exponents, such as 3x⁴ and 5x⁴, then they can simply be added and subtracted. For example, 3x⁴ + 5x⁴ = 8x⁴.

Multiplying and Dividing Numbers with Exponents

To multiply exponential numbers or terms that have the same base, add the exponents together:

To divide two same-base exponential numbers or terms, just subtract the exponents.

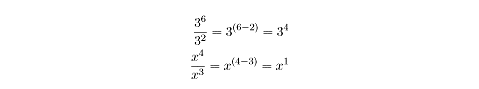
To multiply exponential numbers raised to the same exponent, raise their product to that exponent:

To divide exponential numbers raised to the same exponent, raise their quotient to that exponent:

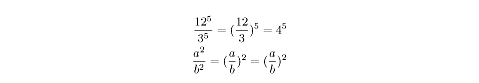
If you need to multiply or divide two exponential numbers that do not have the same base or exponent, you’ll just have to do your work the old-fashioned way: multiply the exponential numbers out and multiply or divide the result accordingly.

Raising an Exponent to an Exponent

Occasionally you might encounter an exponent raised to another exponent, as seen in the following formats (3²)⁴ and (x⁴)³. In such cases, multiply the powers:

(3²)⁴ = (3)² × ⁴ = 3 ⁸ (x⁴)³ = (x)⁴ × ³ = x ¹²

Exponents and Fractions

To raise a fraction to an exponent, raise both the numerator and denominator to that exponent:

Exponents and Negative Numbers

As we said in the section on negative numbers, when you multiply a negative number by another negative number, you get a positive number, and when you multiply a negative number by a positive number, you get a negative number. These rules affect how negative numbers function in reference to exponents.

• When you raise a negative number to an even-number exponent, you get a positive number. For example (–2)⁴ = 16. To see why this is so, let’s break down the example. (–2)⁴ means –2 × –2 × –2 ×–2. When you multiply the first two –2s together, you get +4 because you are multiplying two negative numbers. Then, when you multiply the +4 by the next –2, you get –8, since you are multiplying a positive number by a negative number. Finally, you multiply the –8 by the last –2 and get +16, since you’re once again multiplying two negative numbers.
• When you raise a negative number to an odd power, you get a negative number. To see why, all you have to do is look at the example above and stop the process at –8, which equals (–2)³.

These rules can help a great deal as you go about eliminating answer choices and checking potentially correct answers. For example, if you have a negative number raised to an odd power, and you get a positive answer, you know your answer is wrong. Likewise, on that same question, you could eliminate any answer choices that are positive.

Special Exponents

There are a few special properties of certain exponents that you also need to know.

Zero

Any base raised to the power of zero is equal to 1. If you see any exponent of the form x⁰, you should know that its value is 1. Note, however, that 0⁰ is undefinded.

One

Any base raised to the power of one is equal to itself. For example, 2¹ = 2, (–67)¹ = –67 and x¹ = x. This can be helpful when you’re attempting an operation on exponential terms with the same base. For example:

3x⁶ × x = 3x⁶ × x¹ = ³ =3x^{(6 + 1)} = 3x ⁷

Fractional Exponents

Exponents can be fractions, too. When a number or term is raised to a fractional power, it is called taking the root of that number or term. This expression can be converted into a more convenient form:

Or, for example, 2^{13 / 5} is equal to the fifth root of 2 to the thirteenth power:

⁶ v2¹³ = 6.063

The v symbol is also known as the radical, and anything under the radical, in this case 2 ¹³ ,is called the radicand. For a more familiar example, look at 9^1/2, which is the same as v9

² v9¹ = v9 = 3

Fractional exponents will play a large role on SAT II Math IC, so we are just giving you a quick introduction to the topic now. Don’t worry if some of this doesn’t quite make sense now; we’ll go over roots thoroughly in the next section.

Negative Exponents

Seeing a negative number as a power may be a little strange the first time around. But the principle at work is simple. Any number or term raised to a negative power is equal to the reciprocal of that base raised to the opposite power. For example:

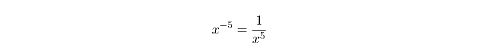
Or, a slightly more complicated example:

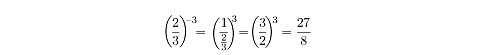
With that, you’ve got the four rules of special exponents. Here are some examples to firm up your knowledge:

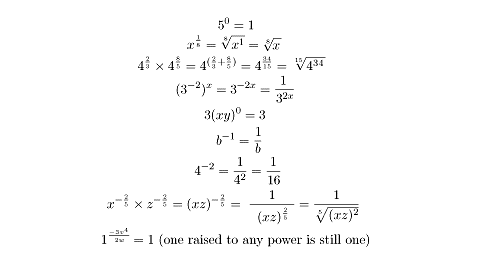
Next to display next topic in the chapter.

Mathematics Practice Questions