Lesson: Data Interpretation - 02

Correlation and Scatter plots

If two variables have a relationship such that when one variable changes, the other changes in a predictable way, the two variables are correlated. For example, there is a correlation between the number of hours an employee works each week and the amount of money the employee earns—the more hours the employee works, the more money the employee earns. Note that in this case, as the first variable increases, the second variable increases as well. These two variables are positively correlated.

Sometimes, when one variable increases, a second variable decreases. For example, the more that a store charges for a particular item, the fewer of that item will be sold. In this case, these two variables are negatively correlated.

Video Correlation and Scatter-plots

Sometimes two variables are not correlated, that is, a change in one variable does not affect the other variable in any way. For example, the number of cans of soda that a person drinks each day is not correlated with the amount of money the person earns.

One way to determine whether two variables are correlated or not is to sketch a scatter plot. A scatter plot is a graph on which the x–axis represents the value of one variable and the y–axis represents the value of the other variable. Several values of one variable and the corresponding values of the other variable are measured and plotted on the graph:

• If the points appear to form a straight line, or are close to forming a straight line, then it is likely that the variables are correlated.
• If the line has a positive slope (right to left), the variables are positively correlated.
• If the line has a negative slope (left to right), the variables are negatively correlated.
• If the points on the scatter plot seem to be located more or less at random, then it is likely that the variables are not correlated.

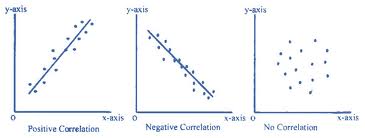
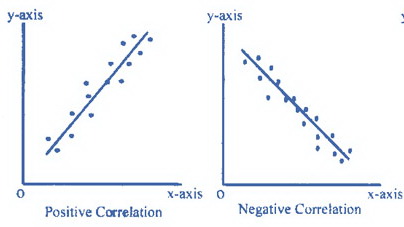
It is rare that the points on a scatter plot will all lie exactly on the same line. However, if there is a strong correlation, it is likely that there will be a line that could be drawn on the scatter plot that comes close to all of the points. Statisticians call the line that comes the closest to all of the points on a scatter plot the “line of best fit.” Without performing any computations, it is possible to visualize the location of the line of best fit, as the diagrams below show:

Next to display next topic in the chapter.