A ratio is a comparison of two numbers. We generally separate the two numbers in the ratio with a colon ":". Suppose we want to write the ratio of 8 and 12.
We can write this as 8:12 or as a fraction 8/12, and we say the ratio is eight to twelve.
Ratio
- The ratio of two quantities a and b of same units is the fraction x/y, where b ? 0
- The fraction x/y can be represented as x:y
Different types of ratios are:
The concept of ratio & proportion is used in quantitative as well as DI section. Grocery shopping, selling, cooking to industries production- everything makes use of the concept of ratio, proportion & mixtures. Partnership assumes significance in the business world, where various business partners need to distribute profits according to their share of investments and time period. Here, you will learn the formulae & shortcuts to solve questions based on ratio, mixtures and partnership.
1) Duplicate ratio:
It is the ratio of squares of two numbers.
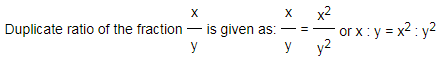
2) Sub-duplicate ratio:
It is the ratio between square roots of two numbers.

3) Triplicate ratio:
It is the ratio of cubes of two numbers.
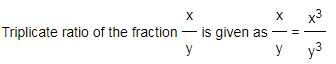
4) Sub- Triplicate ratio:
It is the ratio between cube roots of two numbers
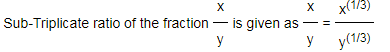
5) Compound ratio:
It is the ratio of product of first terms in every ratio to that of product of second term in every ratio.
For example:
Compound ratio of (a : x), (b : y), (c : z) is (abc : xyz)
6) Inverse ratio:
The ratio formed by interchanging their old places in the ratio to new
The inverse ratio of 5 : 8 is 8 : 5.