It's easy to see that funky radical symbol and panic just a little bit. There are so many rules that go along with it, it's hard to keep up with them all. This lesson will help by describing what you should do when you are faced with a square root.
Follow the Signs
What would happen if you were driving down the road and all of a sudden everyone decided to disregard the road signs? No one was stopping at red lights, worrying about which side of the road they were driving on or even stopping for pedestrians. It would be chaos. There is a reason those signs are there.
What if you drove to the next town to find that their road signs were different from the ones you were used to? They stopped on green lights and, instead of a yield triangle, there was a purple circle. There are rules of the road, but you have no idea what they are or how to follow them. That is why there is a standardized accepted type of road sign for each circumstance.
Mathematics is the same way. There are standardized signs that tell people what to do, and they are the same everywhere. There is no confusion - when you see 8/2, you know to divide, and when you see 3+9, you know that you are supposed to add.
What Are Radicals and Radicands?
The symbol that we are concerned with in this lesson is the radical symbol, or square root. This symbol looks like this:
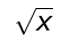
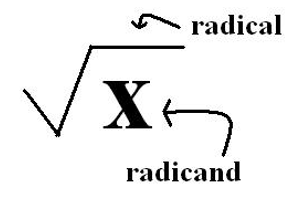
and it tells you to find a number that when multiplied to itself equals the number under the radical symbol. That number under the radical symbol is called the radicand.
What Do Radicals and Radicands Mean?
As you are traveling along the road of mathematics, the radical road sign wants you to take the square root of the term that is inside the symbol, or the radicand. The square root function is the inverse or opposite of the squared function. When you are asked to square a number, you need to take that number and multiply it by itself.
For example:
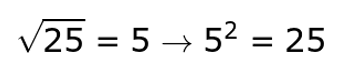
The same rules apply to numbers and variables.
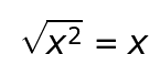
In any expression with a radical symbol, the term under the square root is the radicand - even if the expression is large, like this:
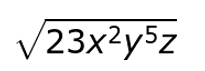
In this example, 23x^2y^5z is the radicand.