Properties of Shapes: Triangles
Isosceles, equilateral and obtuse, oh my! These are terms for triangles. But, what do they mean? In this lesson, we'll explore the properties of triangles and take a closer look at the different types of triangles you may encounter.
Seeing Triangles
Triangles - they're the three-sided shape you see everywhere you look. They're the symbol for play and the sign to slow down. They're the ears on a cat and a slice of pizza. They're the gateway to the unknown and the monument to a long-ago empire.
They're even the musical instrument calling us to dinner if we live on a 19th century farm. Though I don't know how you're watching this online video from a 19th century farm. Let's take a closer look at the many facets of this seemingly simple shape.
Basic Properties
First, let's define what we're talking about. A triangle is a polygon with three sides and three angles. You can remember that triangles have three sides and angles by that 'tri' in the name. 'Tri' means 'three,' whether you're talking about geometry, tricycles or triceratops.
In a triangle, the interior angles always add up to 180 degrees. So, in the triangle below, if one angle is 60 and another is 60, which is 120 total, then the other one has to be 180 - 120, which is also 60. If you ever know two angles of a triangle, you can always find the third by remembering the 180-degree rule.
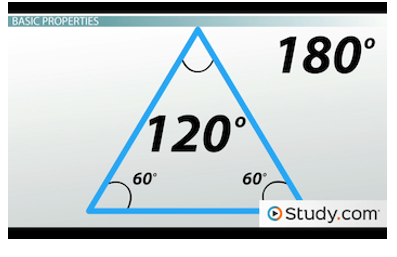
If you know two angles of a triangle, you can determine the third.
Types of Triangles
Triangles that have particular properties get their own names. For example, this one:
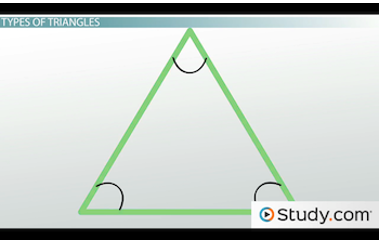
In an equilateral triangle, all the sides and angles are equal<,/p>
Notice that all the angles are the same. As you might guess, there's a direct correlation between the angles and sides. When the angles are all the same, so are the sides. So, this is an example of an equilateral triangle, which is a triangle with three equal sides and three equal angles. Do you hear 'equal' in 'equilateral'? The term literally means 'equal sides.'
Some triangles only have two equal sides. A triangle with two equal sides and two equal angles is called an isosceles triangle. I think of isosceles triangles as an equilateral triangle's younger sibling. Its equalness is not as complete. Note below that the equal sides are always opposite the equal angles. So, if the angles on the bottom are equal, the sides with blue arrows are equal.
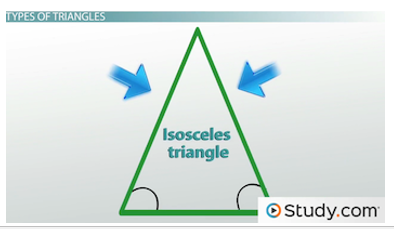
Isosceles triangles have two equal sides and two equal angles.
Then there's the awkward cousin to equilateral and isosceles triangles: the scalene triangle. A scalene triangle is a triangle with no equal sides or angles. Scalene means unequal, but it doesn't sound like unequal. It sounds like 'scale.' Think about yourself on a scale. If you're like me, you probably don't weigh exactly what you'd like to weigh. You're a bit (or more than a bit) off. And, scalene triangles are out of balance, too. None of their sides match.