Lesson: Chapter - 5

Two-Dimensional Motion with Uniform Acceleration

If you’ve got the hang of 1-D motion, you should have no trouble at all with 2-D motion. The motion of any object moving in two dimensions can be broken into x- and y-components. Then it’s just a matter of solving two separate 1-D kinematic equations.

The most common problems of this kind on Physics on the test involve projectile motion: the motion of an object that is shot, thrown, or in some other way launched into the air. Note that the motion or trajectory of a projectile is a parabola.

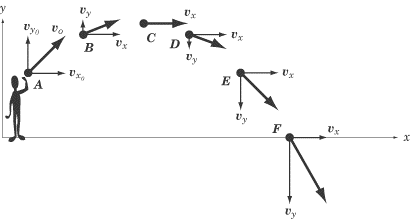
If we break this motion into x- and y-components, the motion becomes easy to understand. In the y direction, the ball is thrown upward with an initial velocity of v_y2 and experiences a constant downward acceleration of g = –9.8 m/s2. This is exactly the kind of motion we examined in the previous section: if we ignore the x-component, the motion of a projectile is identical to the motion of an object thrown directly up in the air.

In the x direction, the ball is thrown forward with an initial velocity of v_x2 and there is no acceleration acting in the x direction to change this velocity. We have a very simple situation where a_x = 0 and v₀ is constant.

Testing Physics will probably not expect you to do much calculating in questions dealing with projectile motion. Most likely, it will ask about the relative velocity of the projectile at different points in its trajectory. We can calculate the x- and y-components separately and then combine them to find the velocity of the projectile at any given point:

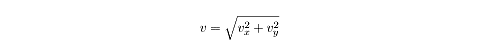
Because v_x is constant, the speed will be greater or lesser depending on the magnitude of v_y . To determine where the speed is least or greatest, we follow the same method as we would with the one-dimensional example we had in the previous section. That means that the speed of the projectile in the figure above is at its greatest at position F, and at its least at position C. We also know that the speed is equal at position B and position D, and at position A and position E.

The key with two-dimensional motion is to remember that you are not dealing with one complex equation of motion, but rather with two simple equations.

Next to display next topic in the chapter.