Lesson: Chapter - 10
Angular Momentum
The rotational analogue of linear momentum is angular momentum,
L. After torque and
equilibrium, angular momentum is the aspect of rotational motion most likely to
be tested on Physics. For the test, you will probably have to deal only
with the angular momentum of a particle or body moving in a circular trajectory.
In such a case, we can define angular momentum in terms of moment of inertia and
angular velocity, just as we can define linear momentum in terms of mass and
velocity:
L = l?
The angular momentum vector always points in the same direction as the angular
velocity vector.
Video Lesson -
Angular Momentum of a Single Particle
Let’s take the example of a tether-ball of mass
m swinging about on a rope of length
r:
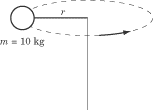
The tether-ball has a moment of inertia of I =
mr2 and an angular velocity of
?
= v/r. Substituting these values
into the formula for linear momentum we get:
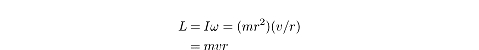
This is the value we would expect from the cross product definition we saw
earlier of angular momentum. The momentum, p
= mv of a particle moving in
a circle is always tangent to the circle and perpendicular to the radius.
Therefore, when a particle is moving in a circle,
L = pr sin90° = pr = mvr
Newton’s Second Law and Conservation of Angular Momentum
In the previous chapter, we saw that the net force acting on an object is equal
to the rate of change of the object’s momentum with time. Similarly, the net
torque acting on an object is equal to the rate of change of the object’s
angular momentum with time:
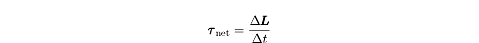
If the net torque action on a rigid body is zero, then the angular momentum of
the body is constant or conserved. The law of conservation of angular
momentum is another one of nature’s beautiful properties, as well as a very
useful means of solving problems. It is likely that angular momentum will be
tested in a conceptual manner on Physics.
Example
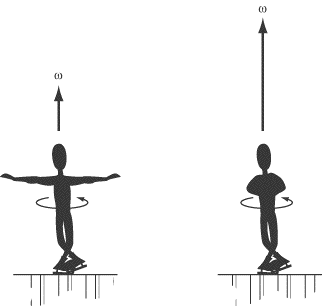
|
|
One of Brian Boitano’s crowd-pleasing skating moves involves initiating a spin
with his arms extended and then moving his arms closer to his body. As he does
so, he spins at a faster and faster rate. Which of the following laws best
explains this phenomenon? |
|
|
(A) |
Conservation of Mechanical Energy |
|
|
(B) |
Conservation of Angular Momentum |
|
|
(C) |
Conservation of Linear Momentum |
|
|
(D) |
Newton’s First Law |
|
|
(E) |
Newton’s Second Law |
Given the context, the answer to this question is no secret: it’s B, the
conservation of angular momentum. Explaining why is the interesting part.
As Brian spins on the ice, the net torque acting on him is zero, so angular
momentum is conserved. That means that I?
is a conserved quantity. I is
proportional to R2, the
distance of the parts of Brian’s body from his axis of rotation. As he draws his
arms in toward his body, his mass is more closely concentrated about his axis of
rotation, so I decreases. Because
I?
must remain constant,
?
must increase as I decreases. As a
result, Brian’s angular velocity increases as he draws his arms in toward his
body.
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.