Problems on Trains

Problems on trains are very common in competitive exams.

Various types of questions are asked on trains. Questions on trains are solved using the concept of time, speed and distance i.e. we use the formulas of time, speed and distance to solve questions on trains.

While studying the chapter “Trains”, we are required to deal with following scenarios:

1. Two trains moving in opposite direction.
2. Two trains moving in same direction.
3. A train crossing a stationary object of a given length like a platform or bridge.
4. A train crossing a stationary object like a pole or a man which can be considered as a point object.

Important Points to Remember

1. If the length of one train is P and the length of second train is Q, the total distance to be covered is (P+Q)
2. 2) Finding Relative speed:
   
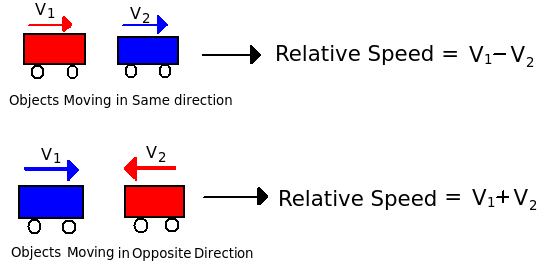
3. If two trains of lengths P and Q move in opposite directions at V₁ m/s and V₂ m/s, then time taken by the trains to cross each other, can be calculated by
   
   
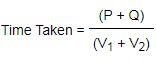
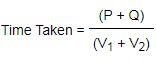
4. If two trains of different lengths P and Q move in same direction at V₁ m/s and V₂ m/s, then time taken by the trains to cross each other, is calculated by

Question 1: A train travelling at 60 kmph crosses a man in 6 seconds. What is the length of the train?

Solution: Speed in m/sec = 60 × (5/18) = 50/3 m/sec

Time taken to cross the man = 6 secs

Therefore, Distance = (50/3)* 6 = 100 metres (i.e. the length of the train)

Question 2: A train travelling at 60 kmph crosses another train travelling in the same direction at 50 kmph in 30 seconds. What is the combined length of both the trains?

Solution: Speed of train A = 60 kmph = 60 × (5/18) = 50/3 m/sec

Speed of train B = = 50 kmph = 50 × (5/18) = 125/9 m/sec

The relative speed =(50/3) - (125/9) = 25/9 m/s (we have subtracted the two values because both the trains are going in the same direction)

Time taken by train A to cross train B = 30 secs

Distance = Speed × Time

Distance =25/9 × 30 = 250/3 metres (i.e. the combined length of both trains)