A decimal number can be defined as a number whose whole number part and the fractional part is separated by a decimal point.

Decimal

Decimal Fractions:Points to Remember

• Fraction: It represents a part of a whole or more generally, any number of equal parts. If a unit is divided into any number of equal parts, then one or more of these parts is termed as a fraction of the unit.
  The numerator in a fraction represents a number of equal parts and denominator (?0) represents how many of those parts make up a unit or a whole.
• The value of fraction (x/y) = 1, if numerator = denominator
• The value of fraction is zero,if numerator=0 and denominator ?0
• The value of fraction is infinity,if the denominator=0
• The value of fraction remains unchanged,even if the numerator and denominator are multiplied or divided by same number
• Pure recurring decimal: In a decimal fraction, if all the numbers after decimal point repeat, then it is called as pure recurring decimal.
• Mixed recurring decimal: In a decimal fraction, if some numbers are repetitive and some are not, then it is called as mixed recurring decimal.

Basic Formulae: (Must Remember)

• 1) (a - b)² = (a² + b² - 2ab)
• 2) (a + b)² = (a² + b² + 2ab)
• 3) (a + b) (a – b) = (a² – b² )
• 4) (a³ + b³) = (a + b) (a² – ab + b²)
• 5) (a³ - b³) = (a - b) (a² – ab + b²)
• 6) (a + b + c)² = a² + b² + c² + 2 (ab + bc + ca)
• 7) (a³ + b³ + c³ – 3abc) = (a + b + c) (a² + b² + c² – ab – bc – ac)

Operations on decimal fractions:

Here different operations performed on decimal fractions along with certain examples are given. Clear the concepts point by point and then move further to quick tips and tricks.
Points covered:
1) Addition and subtraction of decimal fractions
2) Multiplication of decimal fractions by power of 10.
3) Multiplication of decimal fractions.
4) Decimal fraction ÷ Counting number
5) Decimal fraction ÷ Decimal fraction

1) Addition and subtraction of decimal fractions

To add or subtract the decimal fractions, numbers are placed under each other in such a way, that the decimal points lie in one column.
Eg: 12.361 + 0.236 + 1236.1

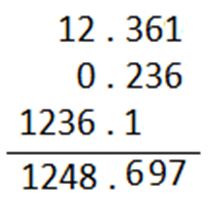
2) Multiplication of decimal fractions by power of 10.

The decimal point in the given number is shifted as many places as is the power of 10.
Eg: 4.236 × 100 = 423.6 or 0.563 × 1000 = 563

3) Multiplication of decimal fractions.

Multiply the given numbers without considering the decimal points. Now mark the decimal point in the product by calculating the sum of number of decimal places in the given numbers.
Eg: 0.5 × 0.03 × 0.83
5 × 3 × 83 = 1245
No. of decimal places = 1 + 2 + 2 = 5
Now mark the decimal point after 5 places starting from left.
Answer = 0.01245

4) Division of a decimal fraction

Divide the given numbers without considering the decimal points. Now mark the decimal point in the quotient obtained, by calculating the number of decimal places in the dividend.
Eg: (0.0133 ÷ 19)
(133 ÷ 19)=7
Dividend contains 4 places of decimal. Hence, the answer is 0.0007

5) Decimal fraction ÷ Decimal fraction

Eg: Divide 0.00025 by 0.5
Convert 0.5 without decimal place i.e. 5. Multiply numerator and denominator by 10.
Therefore, we get
=0.0025 ÷ 5
=0.0005

Comparison of fractions

4/5 = 0.8, 3/5 = 0.6, 6/8 = 0.75
0.8 > 0.75 > 0.6, hence (4/5) > (6/8) > (3/5)