These album covers are rectangles.
Squares
That old album cover fits both the definition of a rectangle and the definition of our next shape, the square. Squares are a very special subset of rectangles. A square is a four-sided shape with all right angles and sides of equal length.
Does that definition look familiar? Here are the steps to define a square: Is it four-sided? Are all the angles 90 degrees? If yes, then you have a rectangle. If all the sides are the same length, then it's not only a rectangle, it's also a square. That means that all squares are rectangles. But not all rectangles are squares, since a rectangle's pairs of sides can have different lengths.
Just like rectangles, squares are everywhere. In addition to the album cover, think about the spaces on a chessboard, stamps, floor tiles and even a snack of crackers and cheese. Because each side of a square has the same length, you don't need to be given much information to solve most problems.
For example, if you see the square below where you know one side is 5, then you know all the other sides are 5 as well. So, the perimeter of this square is 5 * 4, or 20. The area of a square is s^2, or one side squared. So, the area of this square is 5^2, which is 25.
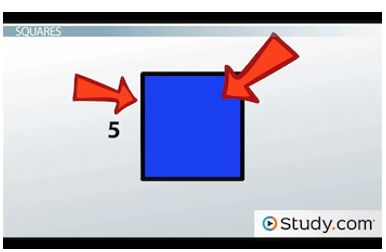
The sides of a square all have the same length.
Rhombuses
Then there is the rhombus. A rhombus is a little different from a square or rectangle. Here are the questions to ask if you think you're dealing with a rhombus: Is it four-sided? Are all the sides equal in length? If both answers are yes, then what you have is a rhombus.
Did you notice what was missing? Right angles. A rhombus doesn't need to have right angles. It can, but that's the big difference with a rhombus. I like to think of it like this: The word 'rhombus' is kind of like the word 'rhino.' If a rhino charges at a square and knocks it askew, it's not a square anymore. But, it is still a rhombus! Rhinos or no, the definition of a rhombus is a four-sided shape with sides of equal length.
There are a few notable properties for rhombuses. First, the opposite sides are parallel. That's true for rectangles and squares, too. But in a rhombus, even if the angles aren't 90 degrees, the opposite sides are still parallel to each other. So, in the one below, AB is parallel to CD. And, AD is parallel to BC. Also, the opposite angles are equal. Here, angle A equals angle C, and angle B equals angle D.
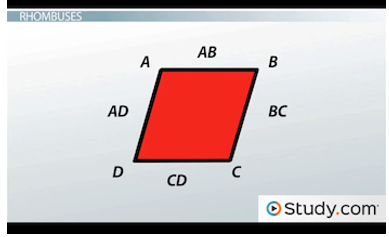
The opposite sides of a rhombus are parallel.
Plus, here's a fun one: If you draw diagonal lines from the corners, those lines form right angles. Since a square is a rhombus, that's true for squares as well. And, no matter how far that rhino pushes the rhombus, those diagonals still form right angles. A square is a rhombus, but a rhombus isn't necessarily a square. And, a rectangle can be a rhombus, but if the sides of a rectangle aren't all equal in length, then it's not a rhombus.
Lesson Summary
In summary, we looked at three different types of quadrilaterals, or four-sided shapes. First, there's the rectangle, which is a four-sided shape with all right angles. Its opposite sides are parallel and equal in length, but each pair of sides isn't necessarily the same length as the other pair.
Second, there's the square, which is a four-sided shape with all right angles and sides of equal length. A square is a type of rectangle, just one where all four sides are the same length. Finally, there's the rhombus, which is a four-sided shape with sides of equal length. The angles can be 90 degrees, but they don't need to be. So, a square is a rhombus, but not every rhombus is a square.