What Are the Five Main Exponent Properties?

Video Lesson on What Are the Five Main Exponent Properties?

What Are the Five Main Exponent Properties?

We'll look at the five important exponent properties and an example of each. You can think of them as the order of operations for exponents. Learn how to handle math problems with exponents here!

Understanding the Five Exponent Properties

We are going to talk about five exponent properties. You can think about them as the order of operations for exponents. Just like the order of operations, you need to memorize these operations to be successful. The five exponent properties are:

The Quotient of Powers property

Product of Powers
Power to a Power
Quotient of Powers
Power of a Product
Power of a Quotient

Let's look at the first one.

Product of Powers

Here's the formula: (x^a)(x^b) = x^(a + b). When you multiply exponentials with the same base (notice that xand x are the same base), add their exponents (or powers).

Let me show you how that works. Let's say I have (x^2)(x^3). Well, x^2 is x times x, and x^3 is x times x times x. When we add all those xs up, we get x^5, which is the same thing as adding 3 + 2.

Power to a Power

The Power of a Product property

We can see from the formula we have (x^a)^b. When you have a power to a power, you multiply the exponents (or powers). Let me show you how this one works.

If I have (x^2)^4, which would be x^2 multiplied four times, or x^2 times x^2 times x^2 times x^2. Once again, we add all the exponents and get x^8, and x^8 is the same as x^(2 * 4), which is 8. Not too bad, right?

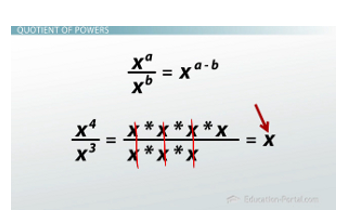
Quotient of Powers

Remember, 'quotient' means 'division'.' The formula says (x^a) / (x^b) = x^(a - b). Basically, when you divide exponentials with the same base, you subtract the exponent (or powers).

Let me show you how this one works. Let's say I had (x^4) / (x^3). In the top (or numerator), we have x times x times x times x. In the bottom (or denominator), we have x times x times x.

Hopefully, you remember that xdivided by x is 1, so the xs cancel. So, x divided by x is 1, x divided by x is 1, and x divided by x is 1. So, when we cancel them, what are we left with? That's right: x^1, or just x. So (x^4) / (x^3) is just x^(4 - 3), which is x^1.

The Power of a Quotient Property

Power of a Product

The formula says (xy)^a = (x^a) and (y^a). When you have a product of a power, you give each base its own exponent. Think about it as distribution putting the exponent with each base.

Let me show you how this one works. Let's say we had (xy)^2. That means we take xy and multiply it twice that means xy times xy. Well, that would give us two xs, or x^2, and two ys, or y^2. That is the same as if I distributed 2 to the x, getting x^2, and 2 to the y, getting y^2.

Power of a Quotient

When we look at this formula, we have x/y, or a fraction raised to the a power, this gives us (x^a) / (y^a). When you have a quotient to a power, you give each base its own exponent. We think of it as the exponent being distributed to each part of the fraction, just like the last one, power of a product.

Let me show you how this one works. Let's say I have (x / y)^3. Remember, that means I'm going to take x / yand multiply it three times. That would be x / y times x / y times x / y. If we look at the top (or the numerator), we have x times x times x, or x^3. If we look at the bottom (or denominator), we have y times ytimes y, or y^3. That would give us (x^3) / (y^3), which is basically distributing 3 to the x and y .

Lesson Summary

Let's take a final minute to review the five properties.

Product of a Power:
When you multiply exponentials with the same base, you add their exponents (or powers).

Power to a Power:
When you have a power to a power, you multiply the exponents (or powers).

Quotient of Powers:
When you divide exponentials with the same base, you subtract the exponents (or powers).

Power of a Product:
When you have a product of a power, you give each base its own exponent (or distribute the exponent to each base).

Power of a Quotient:
When you have a quotient to a power, you give each base its own exponent.

Next Topic

Topics

Next Topic(s)

How to Define a Zero and Negative Exponent

How to Simplify Expressions with Exponents

Rational Exponents

Negative Exponent:

How to Convert Scientific Notation to Standard Form

Jobs in Pakistan Induction process Test Prep Sections Practice MCQs Admission Tests Test Sections Success on Tests Study in USA Pak Universities Employment ISSB Preliminaries Articles and Essays Schools & Colleges Study Abroad Career News

What are the Different Types of Numbers? How to Build and Reduce Fractions What is a Decimal Place Value Statistical Analysis with Categorical Data What is a Variable in Algebra? What Are the Five Main Exponent Properties? What is a Linear Equation? What is an Absolute Value? What are Polynomials, Binomials, and Quadratics? How to Add and Subtract Rational Expressions Perimeter of Triangles and Rectangles Properties of Shapes: Rectangles, Squares and Rhombuses What Is a Number Line? Graph Functions by Plotting Points What is a Linear Equation How to Write Well: What Makes Writing Good? What Are Literary Motifs? How to Evaluate Reasoning Reading Comprehension Techniques for the GMAT How to Organize an Essay How to Structure Sentences in an Essay Using Rhetorical Skills to Write Better Essays How to Write a Great Essay Quickly GMAT Registration Information

Random Topics

MCQ with question Explanations Scholarships and Financial Aid

What Are the Five Main Exponent Properties?

Video Lesson on What Are the Five Main Exponent Properties?