Lesson: Chapter - 4
Fractions
Being able to efficiently and correctly manipulate fractions is essential to
doing well on the Math IC test. A fraction describes a part of a whole.
It is composed of two expressions, a numerator and a denominator. The numerator
of a fraction is the quantity above the fraction bar, and the denominator is the
quantity below the fraction bar. For example, in the fraction
1 /2, 1 is the numerator and 2 is the denominator.
Equivalent Fractions
Two fractions are equivalent if they describe equal parts of the same whole. To
determine if two fractions are equivalent, multiply the denominator and
numerator of one fraction so that the denominators of the two fractions are
equal. For example,
1/2=
3/6because if you multiply the numerator and
denominator of 1 /2by 3, you get:
As long as you multiply or divide both the numerator and denominator of a
fraction by the same nonzero number, you will not change the overall
value of the fraction. Fractions represent a part of a whole, so if you increase
both the part and whole by the same multiple, you will not change their
fundamental relationship.
Reducing Fractions
Reducing fractions makes life with fractions a lot simpler. It takes unwieldy
fractions such as 450 /600 and makes them into smaller,
easier-to-work-with fractions.
To reduce a fraction to its lowest terms, divide the numerator and denominator
by their GCF. For example, for450 /600, the GCF of 450 and 600 is 150. So the
fraction reduces down to 3/4.
A fraction is in reduced form if its numerator and denominator are relatively
prime (their GCF is 1). Thus, it makes sense that the equivalent fractions we
studied in the previous section all reduce to the same fraction. For example,
the equivalent fractions 4/6 and
8/12both reduce to
2/3.
Comparing Fractions
When dealing with integers, large positive numbers with a lot of digits, like
5,000,000, are greater than numbers with fewer digits, such as 5. But fractions
do not work the same way. For example,
200/20,000might seem like a big, impressive
fraction, but
2 /3is actually larger, because 2 is a much bigger
part of 3 than 200 is of 20,000.
In certain cases, comparing two fractions can be very simple. If the
denominators of two fractions are the same, then the fraction with the larger
numerator is bigger. If the numerators of the two fractions are the same, the
fraction with the smaller denominator is bigger.
However, you’ll most likely be dealing with two fractions that have different
numerators and denominators, such as
200/20,000 and
2/3. When faced with this situation, an easy way to
compare these two fractions is to utilize cross-multiplication. All you have to
do is multiply the numerator of each fraction by the denominator of the other,
then write the product of each multiplication next to the numerator you used to
get it. We’ll cross-multiply
200/20,000 and
2/3:
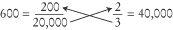
Since 40,000 > 600,
2 /
3 is the greater fraction.
Adding and Subtracting Fractions
On SAT II Math IC, you will need to know how to add and subtract two different
types of fractions. Sometimes you will be given two fractions with the same
denominator, and other times you will have two fractions with different
denominators.
Fractions with the Same Denominators
Fractions can be extremely easy to add and subtract if they have the same
denominator. In addition problems, all you have to do is add up the numerators:

Subtraction works similarly. If the denominators of the fractions are equal,
then you simply subtract one numerator from the other:
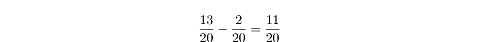
Fractions with Different Denominators
If the fractions do not have equal denominators, the process becomes somewhat
more involved. The first step is to make the denominators the same, and then to
subtract as described above. The best way to do this is to find the least common
denominator (LCD), which is simply the LCM of the two denominators. For example,
the LCD of
1/2 and
2/3 is 6, since 6 is the LCM of 2 and 3.
The second step, after you’ve equalized the denominators of the two fractions,
is to multiply each numerator by the same value as their respective denominator.
Let’s take a look at how to do this for our example,
1/ 2+
2 /3. For
1/2:
numerator = 1 × 3 = 3
denominator = 2 × 3 = 6
So, the new fraction is 3 /6. The same process is repeated for the second
fraction,2 /3:
numerator = 2 × 2 = 2
denominator = 3 × 2 = 6
The new fraction is 4 /6. The final step is to perform the addition or
subtraction. In this case,3/6+ 4/6= 7/6.
If you think it will be faster, you can always skip finding the LCD and multiply
the denominators together to get a common denominator. In some cases, such as
our example, the product of the denominators will actually be the LCD (2 ×
3 = 6 = LCD). But, other times, the product of the denominators will be greater
than the LCD. For example, if the two denominators are 6 and 8, you could use ×
8 = 48 as a denominator instead of 24 (the LCD).
The drawback to this second approach is that you will have to work with larger
numbers and reduce your answer in the end.
Multiplying Fractions
Multiplying fractions is quite simple. The product of two fractions is the
product of their numerators over the product of their denominators.
Symbolically, this can be represented as:
Or, for a numerical example:
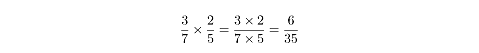
Dividing Fractions
Multiplication and division are inverse operations. It makes sense, then, that
to perform division with fractions, all you have to do is flip the second
fraction , which is also called taking its reciprocal, and then multiply.
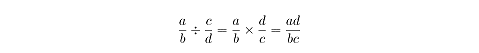
Here’s a numerical example:
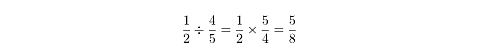
Mixed Numbers
A mixed number is an integer followed by a fraction, like 11/
2. It is another form of an improper fraction, which is a
fraction greater than one. But operations such as addition, subtraction,
multiplication, or division can only be performed on the improper fraction form,
so you need to know how to convert between mixed numbers and improper fractions.
Let’s convert the mixed number 11 /2into an
improper fraction. First, you multiply the integer portion of the mixed number
by the denominator, and add that product to the numerator. So 1 × 2 + 1 = 3, making 3 the numerator of the improper fraction. Now, simply put 3
over the original denominator, 2, and you have your converted fraction.
Here’s another example:
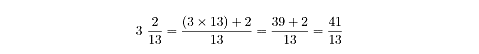
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.