Solving Problems Using Rates
In this video lesson, learn how to set up rate problems so you can easily solve them. You will become familiar with the rate formula and you will see how easy it is to use.
What Is a Rate Problem?
What is a rate problem? A rate problem is a problem involving a rate of some sort, such as speed, earnings, etc. A rate is anything that can be gained or lost over time. You can gain speed over time and you can gain money over time too if you work hard.
Rate problems usually come at you in the form of word problems. I know that word problems are the worst because you have to set up everything yourself. But let me show you how you can easily solve a rate word problem in this video. Keep watching!
So we are looking at our test paper and we see this problem: 'Two brothers want to purchase the next-generation entertainment system that costs $400. How many hours does the brother who makes $12 / hour have to work if the brother who makes $10 / hour can only work for 18 hours?'
See how useful solving rate problems can be? If you have a job and are getting paid on an hourly basis, you can use what you learn in this video lesson to figure out how much you have to work to purchase something you want.
The Rate Formula
Before we can set up our problem, I need to show you what our formula for rate is. Do you remember what rate means? A rate is anything that can be gained or lost over time. There are two ways you can write this mathematically. You can write it using division like so - rate = gain or loss/time - or, you can write it using multiplication like this - gain or loss = rate * time. This also happens to be the most often used form of this formula. Both are the same formula, they're just written differently.
Your rate can be things like your speed or earnings. For our problem, we will use the formula with multiplication because it is the most commonly used form and it's easier for setting up our word problems.
Setting up the Problem
Setting up the problem is the most important step in our solving process. I know, this is the hardest part of word problems, but like I said earlier, don't worry. I'm going to show you an easy way to do it. What we are going to do is make a table showing all of our important information for the problem.
For the table, we are going to follow the format of our rate formula, the one that uses multiplication. Since we are making money, our formula is gain = rate * time. We will call our gain 'earnings' to make it clear that the amount we earn is our gain.
We will have a separate column for each item. We will have a column for gain, a column for our equal sign, a column for rate, a column for our multiplication sign, and a column for the time. We will add an extra column in the beginning to label our brothers. We will call the brother who earns $10 / hour Brother 1 and the brother who earns $12 / hour Brother 2. Our table now looks like this.
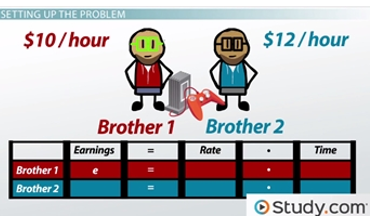
Rate formula set up
Now that we have our table set up, we can fill it in with our information. We will use variables for the boxes we don't know or need to find out. The boxes under earnings are for the total amount earned over a period of time for each brother. We don't know this information, so we will put a variable einto the box for Brother 1. For Brother 2, we will put 400 - e because brother 2 only needs to make the difference between the cost of the entertainment system and the earnings of Brother 1.
For the boxes in the rate column, we will put $10 for Brother 1 and $12 for Brother 2. Under the time column, we will put 18 for Brother 1 since the problem states he can only work for 18 hours. For Brother 2, we will put the variable t because we don't know how much time he needs to work yet. Look at that, we've filled out our table! That wasn't so bad, was it? Now that we have our table filled out, we can go ahead and solve the problem.