Multiplying Binomials Using FOIL and the Area

Video Lesson on Multiplying Binomials Using FOIL and the Area

Multiplying Binomials Using FOIL and the Area Method

From the distributive property, to FOIL, to the area model, to happy faces and claws, there are many different ways to learn how to multiply binomials. In this lesson, you'll learn how to use all of them and get to pick which one you like the most.

What is a Binomial?

Do you know this phrase: 'We all put our pants on the same way: one leg at a time.' It was created to help remind you that you have something in common with all different types of people - movie stars, superstar athletes, homeless people, CEOs; we all put our pants on the same way. But I kind of like it because I like the idea that something is so obviously the right way to do it that everyone does it that way. Sure, you could put your pants on by diving in with both legs right away (and to be honest, I've probably done this in a tent camping or something) but it's clearly the wrong way to go about it. The fact that this phrase has become so well known makes it clear: One leg at a time is without a doubt the best way to put your pants on. So right around now you might be wondering, isn't this an Algebra lesson on multiplying binomials? Why is he talking about pants? Well the reason is that the process for multiplying binomials is the exact opposite of putting your pants on - humans cannot agree on what the best way to do it really is. Instead of there being one obvious way to do it, there are actually tons of different ways. If there was a best way to do it, we wouldn't have come up with so many different strategies. But before we jump right into the strategies, let's start with the basics. What does it mean to multiply binomials?

Multiplying binomials involves 4 mini multiplication problems

Well, a monomial is an algebraic expression with only one term, which makes a binomial an algebraic expression with two, like this: x + 6. We can even have trinomials, expressions with three terms, and bigger ones too. Although the fancy names stop at trinomial and we just start calling them all polynomials no matter how many terms they have, once they have more than three.

Multiplying Binomials

So when we're asked to multiply two binomials, we just need to do something like (x + 2) * (x - 1). Because parentheses next to each other imply multiplication, we can change this into (x + 2)(x - 1).Okay so how do we do it? Well all we really need to do is basically a fancy version of the distributive property. So if I was to look at the problem we have in front of us, but I was to cover up that first x, what we would have is just 2(x - 1), which we could use the distributive property for. It tells us to not only multiply the 2 and the x, but also distribute that 2 to the -1 as well. Whatever is on the outside of the parentheses needs to be multiplied to everything on the inside. So, when I uncover the x and bring it back into my problem, I have to do the exact same thing with it that I just did with the 2: distribute it to both things in the second parentheses. That means first multiplying the x by the x and second, multiplying the x by the -1. This means that anytime you multiply two binomials, it's really just four mini multiplication problems. First I can do x* x to get x2, then I do x * (-1) to get -x, now move on to the 2 and do 2 * x to get a positive 2x and finally, 2 * (-1) to get -2.

The area method is ideal for visual learners

We have now successfully multiplied two binomials, but we are usually going to want to simplify our answer by combining like terms. Grouping the x's together gives us our final answer as x2 + x - 2. And that's it! All the methods we'll go over in the rest of this lesson are simply different ways of remembering how to do all four of those mini multiplication problems. It seems a little silly, but it actually can be easy to forget which mini multiplication problems you've done and which ones you still need to do. So all these little tricks have been developed to help you organize your work and develop a pattern that will prevent you from making those silly mistakes.

The FOIL Method

Let's start with the most well known method: FOIL. This is the method that uses an acronym to help you remember, and it stands for 'firsts, outsides, insides, lasts'. If you say this in your head as you multiply the first terms, the outside terms, inside and last terms, hopefully you'll remember to do all four mini multiplication problems without doing any of them twice. Once we've done the multiplying, we again combine like terms in the end to get our answer.

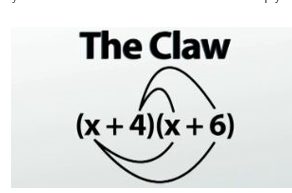
The claw method for multiplying binomials

If you're more of a visual learner like me, you might like the area method more than FOIL. Out of the methods we'll go over, this is probably the safest and surest way to make sure you don't make any mistakes. But it's also probably the most time consuming.

Instead of having you remember an acronym like FOIL, the area method asks you to draw a chart. Because each binomial has two terms, we'll draw a box for the problem (2x + 3)(3x - 1) with two sections on each side. This gives us a box with four regions, one for each mini multiplication problem that we're about to do. Labeling each side with one of the binomials and giving each term its own section lays out all the mini multiplication we need to do. Now we just need to come up with what goes on the inside of the four regions by looking across and above to see which terms are labeled on the outside and multiplying those two things together to get our four mini multiplication problems. Once all four regions have been filled, we can rewrite the expression outside the chart, 6x2 + 9x -3, and combine like terms to get our final answer: 6x2 + 7x - 3.

The Claw and Face Methods

The last two methods we'll go over are simply cute ways we can draw lines right on top of the problem to help us remember which four mini multiplication problems to do. My favorite of these is what I call the claw. By drawing in lines from the first binomial to the second, where each line represents one of the mini multiplications we need to do, we get what looks like a lobster claw. If you draw those same four lines a little bit differently, we can end up with what kinda looks like a smiley face. Each line still represents a mini multiplication problem to do, and once all four have been drawn in, you still must combine like terms to get your final answer.

The face method is yet another visual option for solving problems

So even though we all put our pants on the same way, we all multiply our binomials a little bit differently. That's fine as long as whichever way you pick, you remember to do the correct four mini multiplication problems and then combine your like terms.

Lesson Summary

Binomials are algebraic expressions with two terms, and there are many ways to help you remember how to multiply two of them together. FOIL helps you remember which four mini multiplications to do by being an acronym that stands for 'firsts, outsides, insides, lasts'. The area model helps you remember by giving you a chart with four blank spots to fill in. While the claw and the happy face are pictures you can draw on top of your problem, where each line is one of the mini multiplications you'll need to do. They all work and get you the same answer, so pick your favorite and go for it!

Next Topic

Topics