Subject Math questions that involve inscribed solids don’t require any techniques
other than those you’ve already learned. These questions do require an ability
to visualize inscribed solids and an awareness of how certain line segments
relate to both of the solids in a given figure.
Most often, an inscribed-solid question will present a figure of an inscribed
solid and give you information about one of the solids. For example, you may be
given the radius of a cylinder, and then be asked to find the volume of the
other solid, say a rectangular solid. Using the figure as your guide, you need
to use the radius of the cylinder to find the dimensions of the other solid so
that you can answer the question. Here’s an example:
In the figure below, a cube is inscribed in a cylinder. If the length of the
diagonal of the cube is 4v3
and the height of the cylinder is 5, what is the volume of the cylinder?
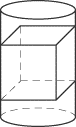
The formula for the volume of a cylinder is pr2(h). The question states that
h = 5, but there is no value given
for r. So in order to solve for the
volume of the cylinder, we need to first find the value of
r.
The key step in this problem is to recognize that the diagonal of a face of the
cube is also the diameter, or twice the radius, of the cylinder. To see this,
draw a diagonal, d, in either the
top or bottom face of the cube.
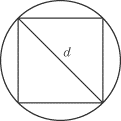
In order to find this diagonal, which is the hypotenuse in a 45-45-90 triangle,
we need the length of an edge of the cube, or s.
We can find s from the diagonal of the cube (not to be confused with the
diagonal of a face of the cube), since the formula for the diagonal of a cube is
sv3 where s is the length of an edge of
the cube. The question states that the diagonal of the cube is 4 v3 so it follows that s = 4. This means
that the diagonal along a single face of the cube is 4v2(using the special properties of a 45-45-90 triangle). Therefore, the radius of
the cylinder is 4v2/2 = 2v2 Plug that into the formula for the volume of the cylinder, and you get p
× (2v22× 5 = 40p.
Helpful Tips
Subject Math questions involving inscribed solids are much easier to solve when you
know how the lines of different solids relate to one another. For instance, the
previous example showed that when a cube is inscribed in a cylinder, the
diagonal of a face of the cube is equal to the diameter of the cylinder. The
better you know the rules of inscribed solids, the better you’ll do on these
questions. So without further ado, here are the rules of inscribed solids that
most commonly appear on the Subject Math.
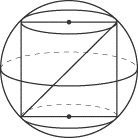
Cylinder Inscribed in a Sphere
The diameter of the sphere is equal to the diagonal of the cylinder’s height and
diameter.
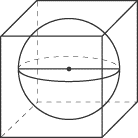
Sphere Inscribed in a Cube
The diameter of the sphere is equal to the length of the cube’s edge.
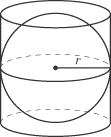
Sphere Inscribed in a Cylinder
Both the cylinder and the sphere have the same diameter and radius.
 Back
Next
Back
Next
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.