Lesson: Chapter - 7
Solids Produced by Rotating Polygons
Another type of Math IC question that you may come across involves a solid
produced by the rotation of a polygon. The best way to explain how this type of
problem works is to provide a sample question:
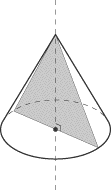
What is the surface area of the geometric solid produced by the triangle below
when it is rotated 360 degrees about the axis AB?
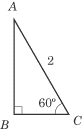
When this triangle is rotated about AB, a cone is formed. To solve the
problem, the first thing you should do is sketch the cone that the triangle will
form.
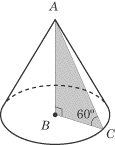
div>
The question asks you to figure out the surface area of the cone. The formula
for surface area is pr2 +
prl, which means you need to know
the lateral height of the cone and the radius of the circle. If you’ve drawn
your cone correctly, you should see that the lateral height is equal to the
hypotenuse of the triangle. The radius of the circle is equal to side BC
of the triangle. You can easily calculate the length of BC since the
triangle is a 30-60-90 triangle. If the hypotenuse is 2, then BC, being
the side opposite the 30º angle, must be 1. Now plug both values of
l and
r into the surface area formula and then simplify:
Total Surface area = p (1)
2 + p (1) (2)
= p + 2p
= 3p
Common Rotations
You don’t need to learn any new techniques or formulas for problems that deal
with rotating figures. You just have to be able to visualize the rotation as
it’s described and be aware of which parts of the polygons become which parts of
the geometric solid. Below is a summary of which polygons, when rotated a
specific way, produce which solids.
|
|
|
|
|
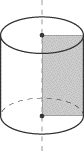
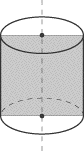
A rectangle rotated about its edge produces a cylinder. |
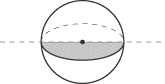
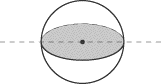
A semicircle rotated about its diameter produces a sphere. |
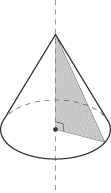
A right triangle rotated about one of its legs produces a cone. |
|
|
|
|
|
A rectangle rotated about a central axis (which must contain the midpoints of
both of the sides that it intersects) produces a cylinder. |
A circle rotated about its diameter produces a sphere. |
An isosceles triangle rotated about its axis of symmetry (the altitude from the
vertex of the non-congruent angle) produces a cone. |
Back
Next
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.