Lesson: Chapter - 9

Explanations

1.D

Since the triangle is a right triangle and the figure gives the value of the angle opposite side AC, you can use the sine function to find the length of AC.

2.B

Since the figure gives only the values for the two legs of this right triangle, to find the measure of <B you’ll first need to calculate a value for tan B and then take the inverse.

which means that

3.C

The kite-flying situation can be modeled by a right triangle with an acute angle of 55º, and a leg opposite that angle whose length is 100 feet. Once you picture the situation as a right triangle, you can see that

where the hypotenuse is the length of the kite string. Therefore, letting x represent the hypotenuse:

4.B

Simplify the left side using trigonometric identities to make this problem easier to solve. First, you need to rearrange the identity sin² x + cos² x = 1 so that you find cos² x – 1 = –sin² x. Then substitute this into the equation. Later, substitute tan x for ^{sin x}/_{cos x}.

Now solve the equation tan x = 1. It’s just a matter of taking the inverse of both sides of the equation:< x = arctan 1 = 45º.

5.B

If ? = ¹/₄ ?, we can rewrite the given conditions: sin ? and cos 4 ? are greater than zero. These are the conditions we must meet.

In order for sin a to be greater than zero, 0º < ? < 180º, because sine is only positive in the first two quadrants. This mean 0 < 4 ? < 720º. Cosine, however, is positive only in the first and fourth quadrants. Thus, for 0º < x < 720º, cosine is only positive in the following intervals: (0º, 90º), (270º, 450º), and (630º, 720º). By dividing these intervals by four, the range of ? is defined: 0º < ? < 22.5º, 67.5º < ? < 112.5º, or 157.5º < ? < 180º. The only answer choice that does not fall within one of these intervals is 65º.

6.C

The variable b adjusts the period of the standard function from 2p to ^2p /_b. The standard sine function, y = sin x, crosses the x-axis three times in the interval 0 = x = 2p: at 0, p, and 2p. So, since the period of a function is the interval between each repeat of the function’s curve, the only way for the graph of y = 3 sin bx to cross the x-axis more often than y = sin x is to have a shorter period. Thus, b must be greater than 1.

To make the function cross the x-axis ⁷/₃ as many times as y = sin x does, you might be tempted to make the period ³ /₇ as long as 2p, which would correspond to a b value of ⁷/₃. This, however, is wrong, because it counts the intersection at 2p too many times. You can check this result if you have a graphing calculator.

By halving the period of the function, you might think that the number of crossings would double. Actually, y = sin 2x crosses the x-axis only five times because the crossing at 2p does not figure into the doubling.

Using this logic as a guide, you see that to achieve seven crossings, you must make the period 3 times shorter so that the first 2 crossings are tripled in number and the crossing at 2p is added at the end. This means that the period of the unknown function is ^2p/₃, and b = 3.

7.A

In the cosine function, the amplitude is the coefficient in front of cosine and the period is 2p divided by the coefficient of x. So for the function y = 2 cos (4x + 2) – 7, the amplitude is 2 and the period is ^2p/₄ = ^p/₂.

8.B

This problem takes a few steps. Your goal is to find AB and the height to vertex C. Then you can use the area formula, A = ¹/₂ bh, where bis the base and his the height.

First, draw an altitude from C to AB.

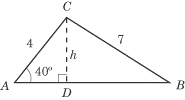
The length of this altitude is the height of the triangle. In the triangle you just formed, triangle ACD, sin 40º = ^h/₄. So, h= 4 sin 40º ˜ 2.57. The Pythagorean theorem can now be used to find lengths AD and BD:

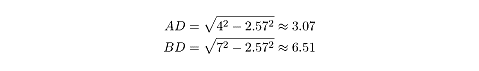
The sum of AD and BD is AB, approximately 9.58. Finally, you can plug these values back into the area formula:

Next to display next topic in the chapter.

Mathematics Practice Questions