These graphs show a number of important characteristics of trigonometric
functions.
Domain
The domain of a function is simply the x values for which the
function can be calculated. In the case of the trigonometric functions, the
input is an angle measure, and the output is a ratio (like opposite/hypotenuse,
for example).
The domain of a trigonometric function can be seen in its graph: it is the set
of all x-values for which the function is defined. For sine and cosine,
the domain is the set of real numbers, because any angle measure has a sine and
a cosine; there are no values of x for which sine or cosine doesn’t
produce a y-value.
The graph of the tangent function, however, tells a different story. It shows
certain x-values for which the tangent is undefined. These undefined
points occur when the cosine is zero, since tan x =
sin x /cos x, and division by zero is
undefined. The x-values for the undefined tangent show up on its graph as
vertical dotted lines every 180º, such that x = n(180º) + 90º,
where n is an integer. For example, the tangent function is undefined at
the x-value 2(180º) + 90º = 450º.
Range
Like the domain, the range of the trigonometric functions can be seen in their
graphs. The range of a function is the set of all possible values of the
function. In other words, the range is the set of all y-values of the
function.
The range of sine and cosine, as you can see in its graph or by analyzing the
unit circle, is –1 = y = 1. The graphs of these two functions never rise
above 1 or fall below –1, and every point on the unit circle has an x and
y value between –1 and 1. Occasionally, you may see a question in which
the answer choices are possible values of sine or cosine. If any of them are
greater than 1 or less than –1, you can eliminate them.
The range of tangent is the set of real numbers. To see why there are no bounds
on the value of tangent, recall that the denominator (cos ? )
can get increasingly close to zero, making the quotient get infinitely large.
The chart below summarizes what has been discussed in the previous few
paragraphs.

Periodic Functions
Sine, cosine, and tangent are all periodic functions, meaning that their values
repeat on a regular interval. This regular interval is called the functions
period. More technically, the period of a function is the smallest domain
containing a full cycle of the function. Take a look at the periods for sine,
cosine, and tangent:
- For y = sin x and y = cos x, the period is 2p
radians. This means that every 360º, the values of sine and cosine repeat
themselves. For example, trigonometric functions of 0 and 2p radians produce the
same values.
- For y = tan x, the period is p radians. Thus, the tangents of 0º
and 180º are equal.
If a trigonometric function contains a coefficient in front of x, its
period changes. In general, the period of y = f(bx) is the
normal period of f divided by b. The period of
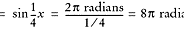
Amplitude
Another useful property of the sine and cosine curves (but not tangent) is
amplitude. The figure below shows the amplitude, a, for the sine and
cosine functions:
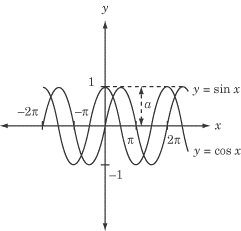
The amplitude of the sine and cosine functions is half the vertical distance
between its minimum value and its maximum value. The amplitude of y = sin
x and y = cos x is 1 because the minimum and maximum values
of these functions are –1 and 1, respectively, and half the vertical distance
between these values is 1. The tangent graph has no amplitude, because the
tangent function has no minimum or maximum value. In general, the amplitude of
the trigonometric function y = af(x) is |a|. The
amplitude of 1/3 cos x is 1/3.
Here is an example of the type of problem on the Math IC that will cover the
graphs of the trigonometric functions.
What is the period and amplitude of the function
y = 4 sin 3
x?
As we just discussed, the period of y = f(bx) is the normal
period of f divided by b. For the sine function, the normal period
is 360o.In this example, b = 3, so the period of this function is 360 ÷ 3
= 120o. In general, the amplitude of the sine function y = af(x) is
|a|. In this particular case, a = 4. So the amplitude is 4.
Take a look at another type of question you may see on the test:
What is the period and amplitude of the function graphed below?
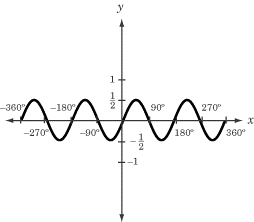
To answer this question, you simply have to read the distances off the graph.
The function, which appears to be either a sine graph or a cosine graph, repeats
itself every 180º. Its period is therefore 180º. Its minimum and maximum values
are ±1/2, so its amplitude is 1/2.
To handle any question about the graphs of trigonometric functions, you should
be able to answer questions about period and amplitude based on the equation or
graph of a given function.
Back
Next
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.