Lesson: Chapter - 14

Energy, Power, and Heat

As a charge carrier moves around a circuit and drops an amount of potential, V, in time t, it loses an amount of potential energy, qV. The power, or the rate at which it loses energy, is qV/t. Since the current, I, is equal to q/t, the power can be expressed as:

P = IV

The unit of power is the watt (W). As you learned in Chapter 4, one watt is equal to one joule per second.

VIR and PIV Triangles

Ohm’s Law and the formula for power express fundamental relationships between power, current, and voltage, and between voltage, current, and resistance. On occasion, you may be asked to calculate any one of the three variables in these equations, given the other two. As a result, good mnemonics to remember are the VIR and PIV triangles:

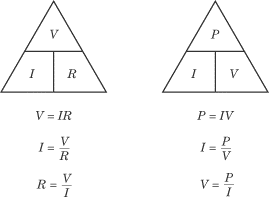
If the two variables you know are across from one another, then multiplying them will get you the third. If the two variables you know are above and below one another, then you can get the third variable by dividing the one above by the one below. For instance, if you know the power and the voltage in a given circuit, you can calculate the current by dividing the power by the voltage.

Power and Resistance

We can combine the equations for power and Ohm’s Law to get expressions for power in terms of resistance:

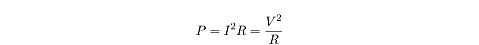
Heat

As current flows through a resistor, the resistor heats up. The heat in joules is given by:

H = I² Rt = Pt

where t is the time in seconds. In other words, a resistor heats up more when there is a high current running through a strong resistor over a long stretch of time.

Example

A circuit with a potential difference of 10 V is hooked up to a light bulb whose resistance is 20 O. The filament in the light bulb heats up, producing light. If the light bulb is left on for one minute, how much heat is produced?

We are being asked for the amount of heat that is dissipated, which is the product of power and time. We have learned to express power in terms of voltage and resistance in the formula P = V²/R. Applying that formula to the problem at hand, we find:

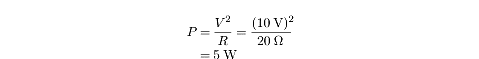
Then, plugging the appropriate numbers into the equation for heat, we find:

H = Pt = (5W)(60 s) = 300 J

Every minute, the filament produces 300 J of heat.

Kilowatt-Hours

When electric companies determine how much to charge their clients, they measure the power output and the amount of time in which this power was generated. Watts and seconds are relatively small units, so they measure in kilowatt-hours, where one kilowatt is equal to 1000 watts. Note that the kilowatt-hour, as a measure of power multiplied by time, is a unit of energy. A quick calculation shows that:

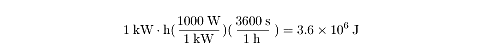
Next to display next topic in the chapter.