Lesson: Chapter - 17

Standing Waves and Resonance

So far, our discussion has focused on traveling waves, where a wave travels a certain distance through its medium. It’s also possible for a wave not to travel anywhere, but simply to oscillate in place. Such waves are called, appropriately, standing waves. A great deal of the vocabulary and mathematics we’ve used to discuss traveling waves applies equally to standing waves, but there are a few peculiarities of which you should be aware.

Reflection

If a stretched string is tied to a pole at one end, waves traveling down the string will reflect from the pole and travel back toward their source. A reflected wave is the mirror image of its original—a pulse in the upward direction will reflect back in the downward direction—and it will interfere with any waves it encounters on its way back to the source. In particular, if one end of a stretched string is forced to oscillate—by tying it to a mass on a spring, for example—while the other end is tied to a pole, the waves traveling toward the pole will continuously interfere with their reflected copies. If the length of the string is a multiple of one-half of the wavelength, ?/2, then the superposition of the two waves will result in a standing wave that appears to be still.

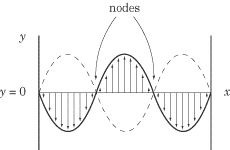
Nodes

The crests and troughs of a standing wave do not travel, or propagate, down the string. Instead, a standing wave has certain points, called nodes, that remain fixed at the equilibrium position. These are points where the original wave undergoes complete destructive interference with its reflection. In between the nodes, the points that oscillate with the greatest amplitude—where the interference is completely constructive—are called antinodes. The distance between successive nodes or antinodes is one-half of the wavelength, ?/2.

Resonance and Harmonic Series

The strings on musical instruments vibrate as standing waves. A string is tied down at both ends, so it can only support standing waves that have nodes at both ends, and thus can only vibrate at certain given frequencies. The longest such wave, called the fundamental, or resonance, has two nodes at the ends and one antinode at the center. Since the two nodes are separated by the length of the string, L, we see that the fundamental wavelength is ?_l = 2L. The string can also support standing waves with one, two, three, or any integral number of nodes in between the two ends. This series of standing waves is called the harmonic series for the string, and the wavelengths in the series satisfy the equation L = n(?/2), or:

?n = 2L/n

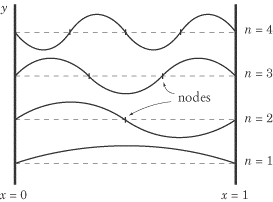
In the figure above, the fundamental is at the bottom, the first member of the harmonic series, with n = 1. Each successive member has one more node and a correspondingly shorter wavelength.

Example

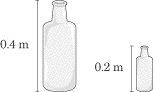
An empty bottle of height 0.2 m and a second empty bottle of height 0.4 m are placed next to each other. One person blows into the tall bottle and one blows into the shorter bottle. What is the difference in the pitch of the two sounds? What could you do to make them sound at the same pitch?

Sound comes out of bottles when you blow on them because your breath creates a series of standing waves inside the bottle. The pitch of the sound is inversely proportional to the wavelength, according to the equation v = ƒ? . We know that the wavelength is directly proportional to the length of the standing wave: the longer the standing wave, the greater the wavelength and the lower the frequency. The tall bottle is twice as long as the short bottle, so it vibrates at twice the wavelength and one-half the frequency of the shorter bottle. To make both bottles sound at the same pitch, you would have to alter the wavelength inside the bottles to produce the same frequency. If the tall bottle were half-filled with water, the wavelength of the standing wave would decrease to the same as the small bottle, producing the same pitch.

Pitch of Stringed Instruments

When violinists draw their bows across a string, they do not force the string to oscillate at any particular frequency, the way the mass on a spring does. The friction between the bow and the string simply draws the string out of its equilibrium position, and this causes standing waves at all the different wavelengths in the harmonic series. To determine what pitches a violin string of a given length can produce, we must find the frequencies corresponding to these standing waves. Recalling the two equations we know for the wave speed, 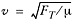and v = ƒ?, we can solve for the frequency, ƒ_n, for any term, n, in the harmonic series. A higher frequency means a higher pitch.

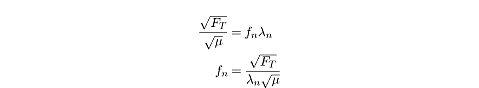
You won’t need to memorize this equation, but you should understand the gist of it. This equation tells you that a higher frequency is produced by (1) a taut string, (2) a string with low mass density, and (3) a string with a short wavelength. Anyone who plays a stringed instrument knows this instinctively. If you tighten a string, the pitch goes up (1); the strings that play higher pitches are much thinner than the fat strings for low notes (2); and by placing your finger on a string somewhere along the neck of the instrument, you shorten the wavelength and raise the pitch (3).

Next to display next topic in the chapter.