Challenging questions in the Quantitative Section may
test your ability to cut through dense information to get to the heart
of what often turns out to be a relatively simple matter. Why does the
Exam do this? To see whether you have the ability to whittle complex language
down to an easy solution. In these problems, the important thing is to
find the "question behind the question." That is, to find what
the question is really asking. Here’s an example:
At the end of every hour a culture of bacteria becomes some
number of times larger than it was the previous hour. If the
number of bacteria was originally greater than 1 and if the
rate of growth also increases every hour, what was the original
number of bacteria?
1) 
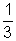of
the original culture would have resulted in a total of 385
bacteria after 3 hours.
2) The original number of bacteria was less than 4.
This problem is really about
.
1) 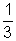of
the original culture would have resulted in a total of
385 bacteria after 3 hours.?
| |
 |
Sufficient |
 |
Insufficient |
|
|
Countinue
What does this mean? Well, if 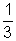of the original culture would’ve
resulted in 385 bacteria after 3 hours, then the actual number of bacteria
must equal 1155 after 3 hours. If we look at this as an equation, we get
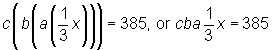. So if we multiply both sides by 3, to get rid of the
fraction, we get cbax = 1155. The product 1155 should set off a
prime factorization alarm, since it contains some primes as factors (most
clearly 5 and 11).
If we divide 1155 by 11, we get 11 × 105,
which gives us 11 ×
5 × 21, which
gives us 11 ×
5 × 7 ×
3. So the prime factorization of 1155 is 3 ×
5 × 7 ×
11. But this is insufficient to tell us which of these numbers is the
original number of bacteria.
We know that the three hourly rates of increase have to be in
increasing size order, but there are four ways to start with one of these
numbers as the original number and the other three as the increasing
rates of growth: 3 ×
5 × 7 ×
11 or 5 ×
3 × 7 ×
11 or 7 ×
3 × 5 ×
11 or 11 ×
3 × 5 ×
7. So Statement (1) is insufficient to tell us what the original number
of bacteria was.
Now let’s look at Statement (2).
Countinue
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ