Lesson: Data Sufficiency Challenging - 22t03

Unexpected Combinations: Example 1

What is the probability that the length of AC is less than or equal to ?

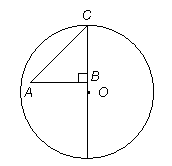
1) The area of circle O is 81.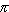

2) The length of AB is 6.

This question deals with two different types of content - probability and geometry. To answer it, we must figure out whether we can determine a probability relationship, so let's start there.

The definition of probability appears below. Use it to determine what we must focus on to solve this question.

Now we must focus on the possible lengths of AC, and we must examine the diagram to do so. Use the diagram to answer the following questions. When you’re ready, click Continue.

• How is AC related to the rest of the diagram?
• What is the relationship between AC and the length ?

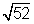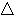We know that ABC is a right triangle. This shouldn’t seem accidental to us. The question itself contains a square root, so the combo of the square root and the right triangle should get us thinking that maybe this question will involve the Pythagorean Theorem. Since AC is the hypotenuse of ABC, 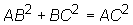. If we want AC to be less than or equal to 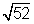, which would mean that AC² is less than or equal to 52, then 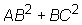must also be less than or equal to 52.

So, basically the question is asking: What is the probability that the hypotenuse of right triangle ABC has a length that is less than or equal to 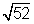? Since the length of the hypotenuse depends on the lengths of the legs of the triangle, we need to determine what the probability is that the legs of the triangle will yield a hypotenuse with a length equal to or less than .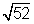

Let’s look at the statements.

Countinue

Next to display next topic in the chapter.