1) x2 has exactly 3 distinct integer factors.
2) x is a prime number.
This question stem is testing both the average formula
and factor knowledge. We'll need to consider both concepts in answering
the question. The average formula appears below. How might we use it to
answer the question?
1) x2 has exactly 3 distinct integer
factors.
| |
 |
Sufficient |
 |
Insufficient |
|
|
Before we spend (read: waste) a lot of time trying out various values,
looking for a perfect square that has only 3 distinct factors we need
to ask ourselves, "What does this statement really tell us about
x?"
If x2 has exactly 3 factors, then those factors
must be 1, x and x2 itself. We know that x2
has only those 3 factors, but what about x? Well, x can’t
have any factors that aren’t also factors of x2. So
the only factors of x must be x itself and the number 1.
What does this mean? That x is prime.
Does knowing that x is prime help us find a single value for
x? Yes, it does. Because we also know from the stimulus that the
average of x’s factors is 6. If we know now that x is prime,
then we know that x has only 2 factors. If x is prime, its only
two factors are 1 and x, and the average of 1 and x is 6, which means
that: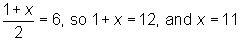 
. Statement 1 is sufficient.
Countinue
Next to display next topic in the chapter.
Test Prep Lessons With Video Lessons and Explained MCQ