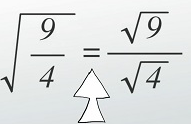Roots and Powers of Algebraic Expressions

In this lesson, you'll learn about some common mistakes that students make when working with roots and powers of algebraic expressions on the SAT and how to make sure you don't fall into the same trap.

Roots and Exponents

Working with roots and exponents can be tricky at the best of times, but when you start adding in algebraic expressions and factoring, it gets even harder. The bad news is that the test writers on the SAT love to throw in problems that throw students for a loop. But the good news is that by learning how to spot these kinds of problems, you can avoid jumping to the wrong conclusions.

In this lesson, you'll learn how to spot two common traps for students working with roots and powers of algebraic expressions. Both of them revolve around distribution properties and order of operations, or the rule that tells us which operation of a given expression to do first. First, we'll go over how these properties work with roots, and then we'll cover how they're applied to exponents.

Roots and Algebra

Roots of algebraic equations can be tricky. The key is to remember when you can distribute the radical and when you can't. Here's the rule: only distribute the radical when the operation underneath is multiplication or division - never with addition or subtraction.

When you have addition or subtraction under the radical sign, you have to do the addition or subtraction before you take the root. The square root of x + y is not the same thing as the square root of x + the square root of y. To illustrate this, let's plug in some real numbers. Let's say x = 16 and y = 9. We'll solve it two ways. On the left is the correct solution and on the right is the incorrect solution.

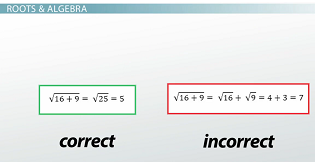
On the left, you first add 16 + 9 to get 25 and then take the square root of that, which is 5. On the right, you can see that if you distribute the radical before doing the addition, you end up with a totally different answer.

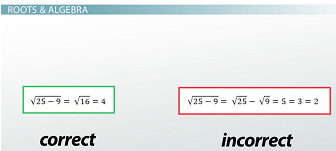
We can do the same thing with subtraction: again, on the left, you first subtract 25 - 9 to get 16, and then you take the square root of that to get 4. But if you do it wrong and distribute the radical before subtracting, you end up with 2 as your answer.

With addition and subtraction, always do the operation underneath the radical before you start worrying about the radical itself. But with multiplication and division, it's different: the square root of x * y is the same thing as the root of x times the root of y. To illustrate this, we'll plug in some numbers: x = 9 and y = 4.

On the left, you take 9 * 4 first to get 36 and then take the square root of that to get 6. On the right, you take the square root of 9 times the square root of 4, which is 3 * 2, which is also 6. As you can see, both of these give you the same answer.

It works the same way with division: the square root of 9/4 is the same thing as the square root of 9 over the square root of 4. So with addition and subtraction, you can't distribute the radical sign. But with multiplication and division, you can.

Powers & Algebra

The exact same rule holds true for powers. For example, when you square an algebraic equation you can't just distribute the square across addition or subtraction. To make this clear, let's plug in some numbers. We'll use x = 3 and y = 4.

On the left is the correct way to do the equation: first add the numbers inside the parentheses and then apply the square. Using this method, we get 49 as the answer.

On the right is the wrong way to do it: distributing the square before adding the numbers inside the parentheses. Using this incorrect method, we get 25. That's a pretty big difference! The same is true for subtraction: (x - y)^2 is not the same thing as x^2 - y^2.

It's all well and good to add the numbers when you actually have numbers, but what if you have an expression like (x + y)^2? Just factor it: (x + y)^2 = (x + y)(x + y). From there, just use FOIL to get x^2 + 2xy + y^2.

And just for the record, it's also worth noting what is equivalent to x^2 - y^2; this is an important equation called the difference of squares. x^2 - y^2 = (x + y)(x - y), not x - y^2. This is a big equation that will show up on the test again, so keep track of it.

Lesson Summary

In this lesson, you learned about some common algebraic errors on the SAT and how to avoid them. When you're working with roots and exponents, it's important to know when you can distribute the root or the power and when you can't. In general, you can only distribute with multiplication or division - not addition or subtraction. The SAT will almost certainly give you at least one problem where you'll have to know this, so just be wary of distributing every root and exponent you see. Don't let the search for an easy answer tempt you into a silly mistake!