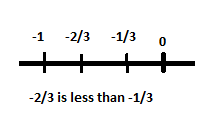Signed Number in Math: Definition & Examples
In this lesson, we will find out about signed numbers. The use of signed numbers could be thought of as where arithmetic ends and algebra begins. We will also discuss situations encountered every day that can be described by using signed numbers.
What Are Signed Numbers?
We will begin an introduction to signed numbers with what is known as the number line. A number line is a horizontal line with incremental marks indicating the position of numbers. The conventional layout for all number lines will have the positive numbers are on the right, the negative numbers are on the left and zero between the negative numbers and the positive numbers. The signed numbers consist of the negative numbers and the positive numbers. We are not used to seeing the (+) sign on positive numbers and most of the time it is not necessary to show it. However, it is always necessary to show the sign on a negative number.
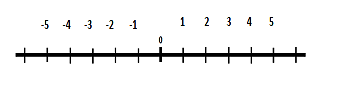
Number Line
Notice that for every positive number, there is a negative counterpart. This is true no matter how small or how large the number is. These counterparts are the same distance from zero. For example, the number 5 and -5 are the same distance from zero. The number 0.0001 and -0.0001 are both the same distance from zero. The number 100,000 and -100,000 are the same distance from zero.
A more precise description for these counterparts is to say that they are opposites or additive inverses. Every number on the number line except zero has an opposite or additive inverse, and it is found by simply changing the sign of the number. The numbers 5 and -5 are opposites or additive inverses. Zero is not considered either negative or positive.
Comparing Values of Signed Numbers
In arithmetic, we learned how to compare positive numbers. We know, for example, that 2 is less than 5. Looking at these values on the number line, we see that 2 is to the left of 5. In fact, notice that the numbers become less in value as you move to the left on the number line and the numbers become greater in value as you move to the right on the number line.
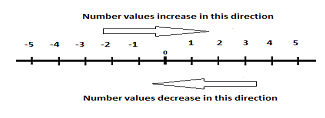
This relationship remains true for numbers on the negative side of the number line as well. For example, -2 is greater in value than -5 because it is farther to the right on the number line.
You have to be especially careful comparing negative fractions and decimals but the same principle applies: numbers farther to the left are less in value and numbers farther to the right are greater in value. For example, -2/3 is less than -1/3 while on the positive side of zero 2/3 is greater than 1/3.