Special Product: Definition & Formula
In this lesson, we will review what a binomial is and how to multiply two binomials together. We will then discuss special cases called special products.
Binomials and FOIL
Binomials are polynomials with two terms. For example:
x + 9
7x - 2y
The two terms in the first binomial are x and 9, and the two terms in the second binomial are 7x and -2y. Binomials are fun to work with in mathematics, because they take on many patterns when we combine them together using various operations. In this lesson, we are going to concentrate on multiplying binomials.
Multiplying binomials may sound like a monumental task, but it's quite easy when we use the FOIL method. FOIL stand for first, inner, outer, last. You are probably wondering what this has to do with multiplying binomials! Well, when we multiply two binomials, like this:
(x + y)(r + s)
We do so by multiplying the first terms of each binomial together to get xr. Then we multiply the outer two terms together to get xs. Next , we multiply the inner two terms together to get yr. Lastly, we multiply the last two terms of each binomial together to get ys, then we add all of these products together to get:
(x + y)(r + s) = xr + xs + yr + ys.
Pretty simple, right? This method is illustrated in the following image.
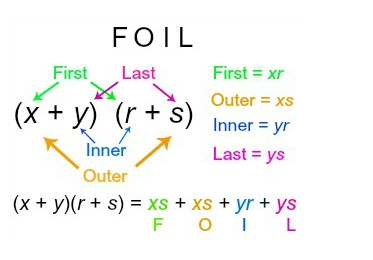
FOIL Method
This process will work for any two binomials, but there are a few special cases where we can simplify this formula even further. These special cases are called special products because they are special cases of products of binomials.
Multiplying the Binomial a + b By Itself
The first special product we will look at is multiplying a binomial by itself. That is:
(a + b)^2 = (a + b)(a + b)
When we perform the FOIL method to this case, we get:
(a + b)(a + b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2
This is illustrated in the following image.
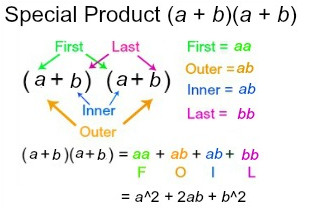
We can use this formula anytime we are multiplying a binomial of the form a + b by itself. For example, consider this binomial:
2x + 1
We use the formula to multiply 2x + 1 by itself to get:
(2x + 1)(2x + 1) = (2x)(2x) + 2(2x*1) + 1*1 = 4x^2 + 4x +1
This formula makes things even simpler, don't you agree? Let's look at another special product.