Roots and Powers of Algebraic Expressions

How to Find the Prime Factorization of a Number

The prime factorization of a number involves breaking that number down to its smallest parts. This lesson will show you two different ways to discover the prime factorization of any number.

Factors of a Number

When you are trying to come to a conclusion about a problem, you often say that there are many 'factors' to consider. This means that there are many parts that make up the whole problem of what you are trying to decide. If the decision is where to go for dinner, the factors involved in that decision might be price, how far away the restaurant is, and how well you will enjoy the food.

Numbers also have factors, the parts that make up the whole number. The factors of a number are the numbers that, when multiplied together, make up the original number.

For example, factors of 8 could be 2 and 4 because 2 * 4 is 8.

And factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24, because 1 * 24 is 24, 2 * 12 is 24, 3 * 8 is 24 and so is 4 * 6. So all of these numbers are said to be factors of 24.

Prime Numbers

A prime number is any number that is only divisible by itself and 1. Some examples of prime numbers include 2, 5 and 17. Numbers such as 15 or 21 are not prime, because they are divisible by more than just themselves and 1.

Prime Factorization

To factor a number is to break that number down into smaller parts. To find the prime factorization of a number, you need to break that number down to its prime factors.

How to Determine the Prime Factorization of a Number

There are two main ways for determining the prime factors of a number. I will demonstrate both methods, and let you decide which you like best.

Both methods start out with a factor tree. A factor tree is a diagram that is used to break down a number into its factors until all the numbers left are prime.

The first way you can use a factor tree to find the factorization of a number is to divide out prime numbers only. Let's factor 24 using this method.

Since 24 is an even number, the first prime number that can be factored out is a 2. This leaves us with 2 * 12. Again, 12 is an even number, so we can factor out another 2, leaving us with 2 * 2 * 6. Since 6 is even, we can factor out a third two, leaving 2 * 2 * 2 * 3.

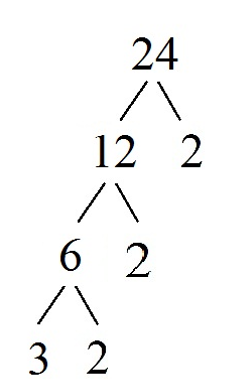
All of these numbers are prime, so the factorization is complete.

The other method for using a factor tree to find the prime factorization of a number is just to pull out the first factors that you see, whether they are prime or not. Looking back at our example from above, let's factor 24 again using this method.

The first thing you might notice is that 6 * 4 is 24, so that is one set of factors for 24. Since neither of these numbers are prime, we can continue to factor both of them. 6 can be broken down to 2 * 3, and 4 can be broken down to 2 * 2. Now all of our factors are prime, and the factorization of 24 is complete, again giving the answer of 2 * 2 * 2 * 3.

Both of these methods work equally well, and can be used interchangeably. There are people who like to use certain tricks to pull out prime numbers first without having to decide what other numbers might be factors of the original number.

The tricks to find some of the prime numbers are:

Any even number is divisible by 2,
2. If you add up the digits in a large number and the sum you get is divisible by 3, the number is also divisible by 3.
3. A number that ends with a 5 or 0 is divisible by 5.

These little tricks can help you factor larger numbers where it might not be easily apparent where to start. Let's try another example.

Find the prime factors of 117.

The first thing I notice about this number is that if you add the digits (1+1+7), you get 9. This means that the number is divisible by 3. Since it is not even, and does not end with a 5 or 0, it is not divisible by 2 or 5, so we can start with the 3.

117 divided by 3 is 39, so our first two factors are 3 and 39. 39 is also divisible by three because 3 + 9 = 12 39/3 equals 13

13 is a prime number, so our factorization is complete, and the factors of 117 are 3 * 3 * 13.

Lesson Summary

The prime factors of a number are all the prime numbers that, when multiplied together, equal the original number. You can find the prime factorization of a number by using a factor tree and dividing the number into smaller parts. You can begin by finding a prime number and factoring out that number, then continuing on in that manner. Or, you can just divide the number into any two numbers, even if they aren't prime and continue on from there until every number is prime.