Lesson: Chapter - 4
Vector Multiplication
There are two forms of vector multiplication: one results in a scalar, and one
results in a vector.
Dot Product
The dot product, also called the scalar product, takes two vectors,
“multiplies” them together, and produces a scalar. The smaller the angle between
the two vectors, the greater their dot product will be. A common example of the
dot product in action is the formula for work, which you will encounter in
Chapter 4. Work is a scalar quantity, but it is measured by the magnitude of
force and displacement, both vector quantities, and the degree to which the
force and displacement are parallel to one another.
The dot product of any two vectors, A
and B, is expressed by the
equation: A.B=AB Cos ?
where ? is the angle made by A and B when they are placed tail to tail.
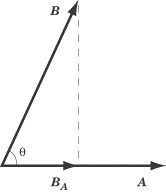
Dot Product remaining
The dot product of A and
B is the value you would get
by multiplying the magnitude of A
by the magnitude of the component of B
that runs parallel to A.
Looking at the figure above, you can get A
· B by
multiplying the magnitude of A
by the magnitude of
BA,
which equals
B Cos ?.
You would get the same result if you multiplied the magnitude of
B by the magnitude of
AB,
which equals
A Cos?.
Note that the dot product of two identical vectors is their
magnitude squared, and that the dot product of two perpendicular vectors is zero.
Example
Suppose the hands on a clock are vectors, where the hour hand has a length
of 2 and the minute hand has a length of 4. What is the dot product of these
two vectors when the clock reads 2 o’clock?
The angle between the hour hand and the minute hand at 2 o’clock is 60°.
With this information, we can simply plug the numbers we have into the formula
for the dot product:
minute hand - hour hand = (2)(4) cos 60° = 4
The Cross Product
The cross product, also called the vector product, “multiplies” two
vectors together to produce a third vector, which is perpendicular to both of
the original vectors. The closer the angle between the two vectors is to the
perpendicular, the greater the cross product will be. We encounter the cross
product a great deal in our discussions of magnetic fields. Magnetic force acts
perpendicular both to the magnetic field that produces the force, and to the
charged particles experiencing the force.
The cross product can be a bit tricky, because you have to think in three
dimensions. The cross product of two vectors,
A and B, is
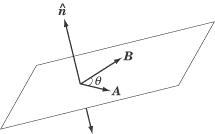
defined by the equation: A × B = AB Sin ? n
where n is a unit vector perpendicular to both A and B.
The magnitude of the cross product vector is equal to the area made
by a parallelogram of A and B. In other words, the greater the area
of the parallelogram, the longer the cross product vector.
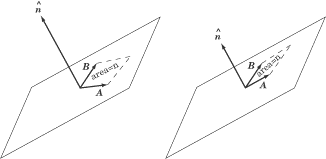
The Right-Hand Rule
You may have noticed an ambiguity here. The two vectors A and B always
lie on a common plane and there are two directions perpendicular to this
plane: “up” and “down.”
There is no real reason why we should choose the “up” or the “down” direction as
the right one, but it’s important that we remain consistent. To that end,
everybody follows the convention known as the right-hand rule. In order
to find the cross product,
A × B
Place the two vectors so their tails are at the same point. Align your right
hand along the first vector, A,
such that the base of your palm is at the tail of the vector, and your
fingertips are pointing toward the tip. Then curl your fingers via the small
angle toward the second vector, B.
If B is in a clockwise
direction from A, you’ll find
you have to flip your hand over to make this work. The direction in which your
thumb is pointing is the direction of
n,
and the direction of
A × B.
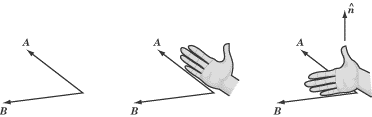
Note that you curl your fingers from A to B because the cross product is A × B .
If it were written B × A, you would have to curl your fingers from B to A, and your
thumb would point downward. The order in which you write the two terms of a cross
product matters a great deal.
If you are right-handed, be careful! While you are working hard on subject test Physics,
you may be tempted to use your left hand instead of your right hand to calculate a
cross product. Don’t do this.
Example
Suppose once again that the minute hand of a clock is a vector of magnitude 4
and the hour hand is a vector of magnitude 2. If, at 5 o’clock, one were to take the
cross product of the minute hand × the hour hand, what would the resultant vector be?
Suppose once again that the minute hand of a clock is a vector of magnitude 4 and
the hour hand is a vector of magnitude 2. If, at 5 o’clock, one were to take the cross
product of the minute handthe hour hand, what would the resultant vector be?
First of all, let’s calculate the magnitude of the cross product vector.
The angle between the hour hand and the minute hand is 150°:
minute hand × hour hand = (2)(4) cos 150°n = 4n
Using the right-hand rule, you’ll find that, by curling the fingers
of your right hand from 12 o’clock toward 5 o’clock, your thumb points
in toward the clock. So the resultant vector has a magnitude of 4 and
points into the clock.
Back
Next
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.